Bu yazı ziyaretçilerimden Oben Işık tarafından yazılmıştır. Oben Işık, İstanbul Teknik Üniversitesi Bilgisayar Mühendisliği ikinci sınıfta okumaktadır. Katkıları için kendisine teşekkür eder, web sitesine bir an önce kavuşmasını dilerim.
Merhaba arkadaşlar, bir localhost yazısı ile daha karşınızdayım.
Sağolsun yazılımportal.com adresindeykenki sponsorumuz Turan İnanır’ın sitemin kapanacağını ve beni yüzüstü bırakacağını 10 gün kala haber vermesinden dolayı artık yazılarımı localhostta yazıp sizlerle paylaşıyorum, yani paylaşacağım.
Bu yazımda ağaç (tree) veri yapısını irdeleyeceğiz, hem de ne irdeleme!
Şunu en baştan söylemekte fayda var; bir çok veri yapısı zaten Standart Template Library (STL) de olan veri yapıları yani hazır olarak var fakat bizim amacımız bedava kullanmayı değil de işin mantığını öğretmek.
Mantığı öğrenmek sizin için çok önemli olacak çünkü belki ilerde başka bir veri yapısını da siz üreteceksiniz ve millet sizin hazır kütüphanenizi kullanacak, hoş olmaz mı? 😀
Öncelikle size ağaç yapımızdaki structlarımızı bir tanıtayım:
[rawr]
struct dugum{
int sayi;
dugum *sol;
dugum *sag;
};
struct agac{
dugum *kok;
int elemansayisi;
void agacolustur();
void ekle(dugum *);
void yazdir();
void preorder(dugum *);
void inorder(dugum *);
void postorder(dugum *);
};
[/rawr]
Şimdi arkadaşlar, öncelikle ben programın tüm kodlarını koymadan önce size biraz structtaki preorder, inorder ve postorder nedir onları anlatayım.
Mesela ağacımız şu şekilde olsun:
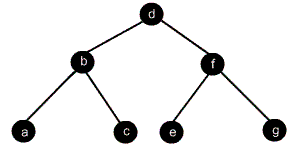
- Sıralı (inorder): İlk adımda sol alt ağaç sıralı şekilde dolaşılır (a-b-c). Kök düğüme uğranır (d). Son adımda sağ alt ağaç sıralı şekilde dolaşılır (e-f-g). Sonuçta ağaç sırasıyla a-b-c-d-e-f-g düğümlerine erişilerek gezilir.
- Kökten Başlayarak (preorder): İlk adımda köke uğranır(d). Sol alt ağaç kökten başlayarak dolaşılır (b-a-c). Son adımda sol alt ağaç kökten başlayarak dolaşılır (f-e-g). Sonuçta ağaç sırasıyla d-b-a-c-f-e-g düğümlerine erişilerek gezilir.
- Sondan Başlayarak (postorder): İlk adımda sol alt ağaç sondan başlayarak dolaşılır (a-c-b). İkinci adımda sağ alt ağaç sondan başlayarak dolaşılır (e-g-f). Son adımda ise köke uğranır(d). Sonuçta ağaç sırasıyla a-c-b-e-g-f-d düğümlerine erişilerek gezilir.
Ve bunların da yanı sıra size sıralı ikili ağaç mantığından bahsetmek istiyorum:
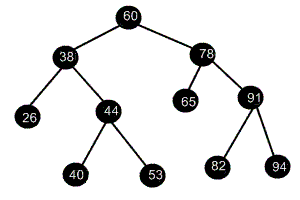
Sıralı ikili ağaçlarda kök hücresinden başlayarak, eğer eklenecek düğümün veri kısmındaki değer, kök düğümünün veri kısmındaki değerden büyük ise sağ tarafa , küçük yada eşit ise sol tarafa eklenir. Bu şekilde olşturulan sıralı ikili ağaçta biliriz ki, sol alt ağaçtaki düğümlerde kökten küçük ya da köke eşit değerler, sağ alt ağaçtaki düğümlerde ise kökten büyük değerler bulunur.
Örneğin üstteki ağaç. 🙂
Şimdi de programımızın kodlarını inceleyelim:
[rawr]
//OBEN ISIK - solid3y3@gmail.com
#include <stdio.h>
#include <stdlib.h>
#include <iostream.h>
using namespace std;
struct dugum{
int sayi;
dugum *sol;
dugum *sag;
};
struct agac{
dugum *kok;
int elemansayisi;
void agacolustur();
void ekle(dugum *);
void yazdir();
void preorder(dugum *);
void inorder(dugum *);
void postorder(dugum *);
};
void agac::preorder(dugum *p){
if(p){
cout << p->sayi << " ";
preorder(p->sol);
preorder(p->sag);
}
}
void agac::inorder(dugum *p){
if(p){
inorder(p->sol);
cout << p->sayi << " ";
inorder(p->sag);
}
}
void agac::postorder(dugum *p){
if(p){
postorder(p->sol);
postorder(p->sag);
cout << p->sayi << " ";
}
}
void agac::agacolustur(){
kok = NULL;
elemansayisi = 0;
cout << "Agac olusturuldu ;) " <<endl;
}
void agac::ekle(dugum *eklenecek){
bool eklendi = false;
dugum *tara; dugum *yeni = new dugum;
tara = kok;
*yeni = *eklenecek; yeni->sol = NULL; yeni->sag = NULL;
if(kok == NULL){
kok = yeni;
cout << "Ilk eleman eklendi ! (" << kok->sayi << ")"<<endl;
elemansayisi++;
return;
}
while((tara != NULL) && (!eklendi))
{
if( yeni->sayi < tara->sayi)
{
if(tara->sol != NULL) { tara = tara->sol; }
else
{
cout << tara->sayi << " dugumunun soluna " << yeni->sayi << " elemanini ekledim, sanirim :D" << endl;
tara->sol = yeni;
eklendi = true;
}
}
else if ( yeni->sayi > tara->sayi)
{
if(tara->sag != NULL) tara = tara->sag;
else
{
cout << tara->sayi << " dugumunun sagina " << yeni->sayi << " elemanini ekledim, sanirim :D " << endl;
tara->sag = yeni;
eklendi = true;
}
}else { cout << "Kopya" << endl; return;}
}
if(eklendi == true) { elemansayisi++; }
cout << "Eleman sayisi : " << elemansayisi << endl ;
cout << "PREORDER :\t\t"; preorder(kok);
cout << endl;
cout << "INORDER :\t\t"; inorder(kok);
cout << endl;
cout << "POSTORDER :\t\t"; postorder(kok);
cout << endl;
}
int main(){
typedef agac veriyapisi;
veriyapisi kayit;
dugum yenikayit;
kayit.agacolustur();
for(int i=1;i<10 ;i++){
cout << endl << "Eleman : ";
cin>>yenikayit.sayi;
kayit.ekle(¥ikayit);
}
system("pause");
return 0;
}
[/rawr]
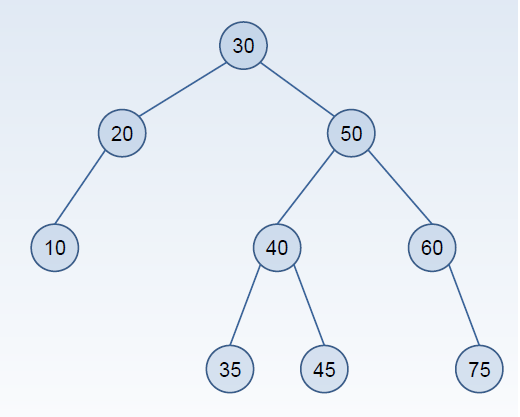
Kodlardan da anlaşılabileceği gibi aslında mantığı çok basit, yukarıdaki ağacı programımızla oluşturalım ve preorder , inorder ve postorder durumlarını inceleyelim.
Ağacımıza ilişkin veriler programa girildiğinde;
[rawr]
Agac olusturuldu ;) Eleman : 30 Ilk eleman eklendi ! (30) Eleman : 20 30 dugumunun soluna 20 elemanini ekledim, sanirim :D Eleman sayisi : 2 PREORDER : 30 20 INORDER : 20 30 POSTORDER : 20 30 Eleman : 50 30 dugumunun sagina 50 elemanini ekledim, sanirim :D Eleman sayisi : 3 PREORDER : 30 20 50 INORDER : 20 30 50 POSTORDER : 20 50 30 Eleman : 10 20 dugumunun soluna 10 elemanini ekledim, sanirim :D Eleman sayisi : 4 PREORDER : 30 20 10 50 INORDER : 10 20 30 50 POSTORDER : 10 20 50 30 Eleman : 40 50 dugumunun soluna 40 elemanini ekledim, sanirim :D Eleman sayisi : 5 PREORDER : 30 20 10 50 40 INORDER : 10 20 30 40 50 POSTORDER : 10 20 40 50 30 Eleman : 60 50 dugumunun sagina 60 elemanini ekledim, sanirim :D Eleman sayisi : 6 PREORDER : 30 20 10 50 40 60 INORDER : 10 20 30 40 50 60 POSTORDER : 10 20 40 60 50 30 Eleman : 35 40 dugumunun soluna 35 elemanini ekledim, sanirim :D Eleman sayisi : 7 PREORDER : 30 20 10 50 40 35 60 INORDER : 10 20 30 35 40 50 60 POSTORDER : 10 20 35 40 60 50 30 Eleman : 45 40 dugumunun sagina 45 elemanini ekledim, sanirim :D Eleman sayisi : 8 PREORDER : 30 20 10 50 40 35 45 60 INORDER : 10 20 30 35 40 45 50 60 POSTORDER : 10 20 35 45 40 60 50 30 Eleman : 75 60 dugumunun sagina 75 elemanini ekledim, sanirim :D Eleman sayisi : 9 PREORDER : 30 20 10 50 40 35 45 60 75 INORDER : 10 20 30 35 40 45 50 60 75 POSTORDER : 10 20 35 45 40 75 60 50 30 Devam etmek için bir tuşa basın . . .
[/rawr]
şeklinde bir ekran görüntüsü oluşur.
Şimdi de ağacımızda rakam aramaya çalışalım. Kodları vermeden önce sonucu vermek istiyorum:
[rawr]
Eleman sayisi : 9 PREORDER : 30 20 10 50 40 35 45 60 75 INORDER : 10 20 30 35 40 45 50 60 75 POSTORDER : 10 20 35 45 40 75 60 50 30 Hangi elemani ariyorsunuz ? : 35 ARADIGIM : 35 Siz 35 girdiniz ve ben de 35 elemanini 4.denemede buldum ;) Devam etmek için bir tuşa basın . . .
[/rawr]
Şimdi program böyle diyor, bakalım 4. denemede bulmuş muyuz? İrdeleyelim:
- 30 ile 35 karşılaştırıldı, 35 > 30, o yüzden sağa dallanmalıyız.
- 30 ile 50 karşılaştırıldı, 30 < 50, o yüzden sola dallanmalıyız.
- 30 ile 40 karşılaştırıldı, 30 < 40, o yüzden sola dallanmalıyız.
- 35 ile 35 karşılaştırıldı, TRUE RESULT!
Peki ya olmayan bir değeri aramaya çalışsak ne olacaktı? Ben denedim programda ve böyle bir sonuç çıktı:
[rawr]
Hangi elemani ariyorsunuz ? : 100 ARADIGIM : 100 Olmayan deger aradin eline ne gecti ? Devam etmek için bir tuşa basın . . .
[/rawr]
Kodları merak ediyorsunuz dimi, 😀 aslında mantığı tamamen ekleme ile aynı, inceleyince siz de anlayacaksınız.
[rawr]
void agac::ara(dugum *eklenecek){
dugum *tara;
tara = kok;
bool bulundu = false;
int kacinci = 1;
cout << "ARADIGIM : " << eklenecek-> sayi <<endl ;
while((tara != NULL) && !bulundu){
if(eklenecek->sayi < tara->sayi)
{
tara = tara->sol;
kacinci++;
}
else if(eklenecek->sayi > tara->sayi)
{
tara = tara->sag;
kacinci++;
}
else { cout << "Siz " << eklenecek->sayi << " girdiniz ve ben de " << tara->sayi << " elemanini "<< kacinci << ".denemede buldum ;) " << endl; return;}
}
cout << "Olmayan deger aradin eline ne gecti ? " << endl;
}
[/rawr]
Not: struct yapımıza fonksiyonumuzu tanıtmayı unutmuyoruz, main fonksiyonumuzdan da aranacak elemanı aşağıdaki şekilde göndertebiliriz:
[rawr]
cout << "Hangi elemani ariyorsunuz ? : " ;
int aranan;
cin >> yenikayit.sayi;
kayit.ara(¥ikayit);
[/rawr]
Buraya kadar sanırım bir çok birşey öğrendik.
Ağaç yapısında veri silme başlı başına bir olay oldugu için başka bir konuda başlıca değineceğiz.
Umarım bu bilgileri iyi harmanlarsınız çünkü ilerde çok işinize yarayacak bence. 😀
İyilikler dilerim, OBEN IŞIK.





Ağaç Veri Yapısı [C++ Örnek] 34 yorum aldı.
öncelikle paylaşımınız için teşekkürler.
bu kodların bir de silme fonksiyonlu olanı var mıdır elinizde ?
Ulan bu ne biçim konu anlatım tarzı
Almanya’da nasıl ehliyet aldım?
‘de, da’ eki nasıl yazılır?
Almanya’dan kalıcı oturuma izni (niederlassungserlaubnis) nasıl alınır?
Harici monitör parlaklığı klavye ile nasıl değiştirilir?
Almanya’da nasıl ehliyet aldım?
Bir şirket neden uzaktan çalışmaya (remote working) izin verir?
-de -da eki ne zaman ayrı yazılır?
Almanya’ya gelmek için yapılan bürokratik işlemler